Dual numbers

By horsing around on YouTube these days I found this video about dual numbers, which I found actually quite interesting. Since I have a computer engineering background, I immediately asked myself what can these numbers used for. It turns out, for some pretty nifty stuff.

What dual numbers are

Essentialy, they are expressions of the form¹

$$ a + b\varepsilon \quad\quad a\in\R, b\in\R, \varepsilon^2 = 0 $$

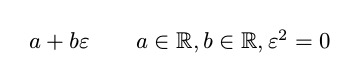
Addition and multiplication are straightforward

$$ \begin{align*} (a + b\varepsilon) + (c + d\varepsilon) &= (a + c) + (b + d)\varepsilon \\ (a + b\varepsilon)(c + d\varepsilon) &= ac + (ad + bc)\varepsilon \end{align*} $$

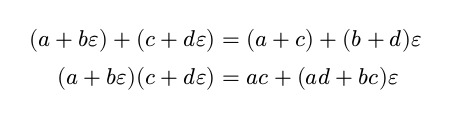
If we define the conjugate of a dual number 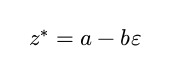$z$ as $z^* = a - b\varepsilon$, we can define its absolute value as

$$ |z|^2 = zz^* = a^2 $$

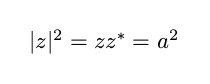
And division is very similar to the complex numbers case

$$ \begin{align*} \frac{a+b\varepsilon}{c+d\varepsilon} &= \frac{a+b\varepsilon}{c+d\varepsilon}\frac{c-d\varepsilon}{c-d\varepsilon} \ &= \cdots \ &= \frac{a}{c} + \frac{bc - ad}{c^2}\varepsilon \end{align*} $$

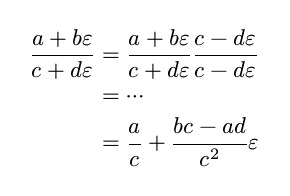
What are they useful for

There are various uses, but one example could be automatic differentiation.

As highlighted both in the previous video and on Wikipedia, given any real polynomial $ P(x) $ it's straightforward to extend its to domain to the dual numbers, and then you can obtain the following

$$ P(x + \varepsilon) = P(x) + \varepsilon P'(x) $$

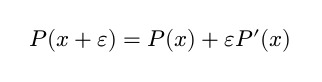
Where $P'(x)$ is the first derivative of $P$ in $x$. Essentialy, you can in one pass compute both the value of a (polynomial) function and the value of its derivative in a specific point.

Trying to put everything into Haskell

For this I've used the GADTs language extension, so that I can use all numeric types to build the Dual datatype. The definition is pretty simple

{-# LANGUAGE GADTs #-}

data Dual a where
  (:+) :: Num a => a -> a -> Dual a

eps :: Num a => Dual a
eps = 0 :+ 1 -- A little utility for later

Here it's necessary to define Dual a and not only Dual, otherwise we'll run into some problems when defining instances. A downside of using a GADT is having to define manually (or standalone-derive) the Show instance.

instance Show a => Show (Dual a) where
  show (a :+ b) = show a <> " :+ " <> show b

So, dual numbers are numbers after all, so a Num and a Fractional instances won't hurt², and they are pretty much a translation of the rules we seen before

instance Num a => Num (Dual a) where
  (a :+ b) + (c :+ d) = (a + c) :+ (b + d)
  (a :+ b) * (c :+ d) = (a * c) :+ (a*d + b*c)
  fromInteger n       = fromInteger n :+ 0
  negate x            = fromInteger (-1) * x
  abs (a :+ _)        = abs a :+ 0
  signum              = undefined

instance Fractional a => Fractional (Dual a) where
  fromRational n = fromRational n :+ 0
  (a :+ b) / (c :+ d) = (a / c) :+ ((b*c - a*d) / c ^ 2)

Finally, we can test if it all works by using a simple polynomial function and its derivative

$$ \begin{aligned} f(x) &= 3x^2 - 4x \ f'(x) &= 6x - 4 \end{aligned} $$

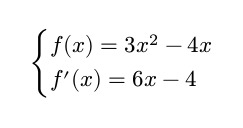
Let's try some random inputs

Finally, we can define all the necessary functions in Haskell³

xs = [0, 1, -1, 7, 3, -2]

diff :: (Num a, Num b) => (Dual a -> b) -> Dual a -> b
diff f x = f (fromInteger x + eps)

xs' = map (diff f) xs

Now we get

ghci> mapM_ print xs'
0 :+ -4
-1 :+ 2
7 :+ -10
119 :+ 38
15 :+ 14
20 :+ -16

Which are all correct! We can see that the "real" part of the numbers is the value of $f$ in the specific point, while the "epsilon" part is the value of $f'$ in the same point.

I think it's really nice how these things arise from well defined and surprisingly simple rules and definitions.

The full code: